题解 P1345 [USACO5.4]奶牛的电信Telecowmunication

发表于 | 更新于

题意：求网络流图中最小割点

一开始题意看成最小割边，把板子改了一下直接交，80(这样都能有80)

我们可以考虑“拆点”，即把一个点拆成两个点，中间连一条边权为1的边。

前一个点作为“入点”，别的点连边连入这里。

后一个点作为“出点”，出去的边从这里出去。

这样，只要我们切断中间那条边，就可以等效于除去这个点

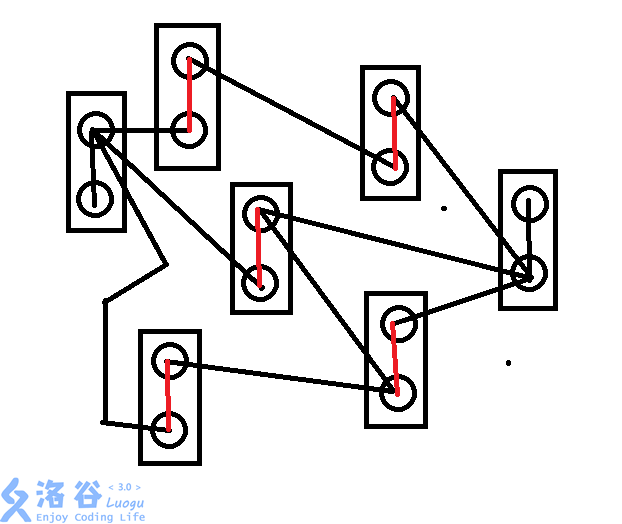
红色的边边权为$1$，黑色的边边权为$inf$。

原点和汇点的内部边权为$inf$，因为显然这两个点不能删除。

题面给的边删除没意义（因为我们要删点），所以也设为$inf$

网络流建反向边只是为了有”反悔”的机会，确保答案最优，所以在已有反向边时就没有必要建边圈为$0$的反向边了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
#include <bits/stdc++.h>
#define ll long long
using namespace std;
struct node{
    int to,dis,next;
}e[400000];
inline int read(){
   int x=0,w=0;char ch=getchar();
   while (!isdigit(ch))w|=ch=='-',ch=getchar();
   while (isdigit(ch))x=(x<<1)+(x<<3)+ch-'0',ch=getchar();
   return w?-x:x;
}
int vis,res,cnt=1,head[400000],inque[400000],dep[400000],n,m,s,t;
inline void add(int u,int v,int d){
    e[++cnt].to=v;
    e[cnt].next=head[u];
    e[cnt].dis=d;
    head[u]=cnt;
}
inline int bfs(){
    memset(dep,0x3f,sizeof(dep));
    memset(inque,0,sizeof(inque));
    queue<int>q;q.push(s);
    dep[s]=0;
    while (!q.empty()){
        int u=q.front();q.pop();inque[u]=0;
        for (int i=head[u];i;i=e[i].next){
            int v=e[i].to;
            if (e[i].dis&&dep[v]>dep[u]+1){
                dep[v]=dep[u]+1;
                if (v==t)return 1;
                if (!inque[v]){
                    q.push(v);inque[v]=1;
                }
            }
        }
    }
    return dep[t]<0x3f3f3f3f;
}
int dfs(int u,int mn){
    if (u==t) return mn;
    int mi=0,used=0;
    for (int i=head[u];i;i=e[i].next){
        int v=e[i].to;
        if (e[i].dis&&dep[v]==dep[u]+1){
            if (mi=dfs(v,min(mn-used,e[i].dis))){
                used+=mi;
                e[i].dis-=mi;
                e[i^1].dis+=mi;
                if (used==mn)break;
            }
        }
    }
    return used;
}
inline int Dinic(){
    int x;
    while (bfs())
        while (x=dfs(s,0x3f3f3f3f))res+=x;
    return res;
}
int main(){
    n=read(),m=read(),s=read()+n,t=read();
    for (int i=1;i<=n;++i)add(i,i+n,1),add(i+n,i,0);
    for (int i=1;i<=m;++i){
        int u=read(),v=read();
        add(u+n,v,0x3f3f3f3f);
        add(v+n,u,0x3f3f3f3f);
    }
    printf("%d",Dinic());
    return 0;
}